CUDA Programming

Problem plecakowy z wykorzystaniem przetwarzania równoległego

Posted May 16, 2025 Updated May 19, 2025

By Szymon Tadych

8 min read

CUDA Programming

Opis Projektu

Algorytm do rozwiązania wariantu problemu plecakowego (każdy przedmiot charakteryzuje się wagą, wartością oraz dodatkową funkcją priorytetu). Należy wybrać podzbiór przedmiotów, którego łączna waga nie przekracza limitu, a łączna ocena (mogąca być sumą wartości lub uwzględniać funkcję priorytetu) jest maksymalizowana. Celem projektu jest porównanie czasu wykonania poszczególnych wersji oraz analiza ich efektywności i skalowalności.

Funkcja oceny rozwiązania

Funkcja oceny rozwiązania jest określona przez:

\[V = \sum (v_i + p_i \cdot F)\]

gdzie:

\(v_i\) - wartość przedmiotu,
\(p_i\) - priorytet przedmiotu,
\(F\) - współczynnik priorytetu,
\(S\) - zbiór wybranych przedmiotów.

Lp	Algorytm (KOD)	Kategoria	Przeznaczenie	Uwagi
1	KS1	Sekwencyjny	Pełny przegląd	Złożoność: O(2ⁿ)
2	KO1	Równoległy (OpenMP)	Pełny przegląd równoległy	Złożoność: O(2ⁿ/p)
3	KC1	GPU (CUDA)	Pełny przegląd na GPU	Złożoność: O(2ⁿ/t)

Opis algorytmu sekwencyjnego

Algorytm KS1:

Dane:

items - lista przedmiotów,
capacity - pojemność plecaka,
priorityFactor - współczynnik priorytetu.

Wynik:

maksymalna wartość wybranych przedmiotów.

Metoda:

Wygeneruj wszystkie możliwe podzbiory \((2^n/t)\).
Dla każdego podzbioru:
- Oblicz całkowitą wagę.
- Jeśli waga <= capacity:
  - Oblicz wartość z priorytetem \(V = \sum (v_i + p_i \cdot F)\).
  - Zapamiętaj maksymalną wartość.
Zwróć najlepsze rozwiązanie.

Złożoność: \(O(2^n)\)

Opis algorytmu równoległego OpenMP

Algorytm KO1:

Dane:

items - lista przedmiotów,
capacity - pojemność plecaka,
priorityFactor - współczynnik priorytetu.

Wynik:

maksymalna wartość wybranych przedmiotów.

Metoda:

Podział przestrzeni przeszukiwania \((2^n)\) na wątki.
Dla każdego wątku:
- Przydziel zakres podzbiorów do sprawdzenia.
- Dla każdego podzbioru w zakresie:
  - Oblicz całkowitą wagę.
  - Jeśli waga <= capacity:
    - Oblicz wartość \(V = \sum (v_i + p_i \cdot F)\).
    - Zapamiętaj lokalne maksimum.
Synchronizacja i wybór globalnego maksimum.

Złożoność: \(O(2^n / p)\), gdzie \(p\) to liczba wątków.

Skalowalność: Liniowa względem liczby rdzeni CPU.

Opis algorytmu CUDA

Algorytm KC1:

Dane:

items - lista przedmiotów,
capacity - pojemność plecaka,
priorityFactor - współczynnik priorytetu.

Wynik:

maksymalna wartość wybranych przedmiotów.

Metoda:

Skopiuj dane przedmiotów na pamięć GPU.
Dla każdego wątku GPU:
- Wyznacz unikalny podzbiór do sprawdzenia.
- Oblicz całkowitą wagę podzbioru.
- Jeśli waga <= capacity:
  - Oblicz wartość \(V = \sum (v_i + p_i \cdot F)\).
  - Zapisz wynik w tablicy wartości.
Wykonaj redukcję równoległą do znalezienia maksimum.
Skopiuj wynik końcowy na CPU.

Złożoność: \(O(2^n / t)\), gdzie \(t\) to liczba wątków GPU.

Skalowalność: Zależna od liczby rdzeni CUDA.

Kod projektu

Wersja sekwencyjna (kompilacja: g++ knapsack_seq.cpp -o knapsack_seq -O2)

  
#include <iostream>
#include <vector>
#include <cstdint>
#include <random>
#include <ctime>
 
struct Item {
    int weight;
    int value;
    int priority;
};
 
std::vector<Item> generateItems(int numItems) {
    std::vector<Item> items;
    std::mt19937 rng(static_cast<unsigned>(std::time(nullptr)));
    std::uniform_int_distribution<int> wDist(1, 50);
    std::uniform_int_distribution<int> vDist(1, 100);
    std::uniform_int_distribution<int> pDist(1, 5);
 
    for (int i = 0; i < numItems; ++i) {
        items.push_back({wDist(rng), vDist(rng), pDist(rng)});
    }
    return items;
}
 
int evaluateSolution(const std::vector<Item>& items, uint64_t mask, int capacity, double priorityFactor, bool& valid) {
    int totalWeight = 0;
    int totalValue = 0;
    for (size_t i = 0; i < items.size(); i++) {
        if (mask & (1ULL << i)) {
            totalWeight += items[i].weight;
            totalValue  += items[i].value + static_cast<int>(items[i].priority * priorityFactor);
            if (totalWeight > capacity) {
                valid = false;
                return 0;
            }
        }
    }
    valid = true;
    return totalValue;
}
 
int main() {
    int numItems = 30;
    int capacity = 400;
    double priorityFactor = 0.5;
 
    std::vector<Item> items = generateItems(numItems);
    uint64_t totalSubsets = 1ULL << numItems;
 
    int bestValue = 0;
    uint64_t bestMask = 0;
 
    for (uint64_t mask = 0; mask < totalSubsets; ++mask) {
        bool valid = false;
        int value = evaluateSolution(items, mask, capacity, priorityFactor, valid);
        if (valid && value > bestValue) {
            bestValue = value;
            bestMask = mask;
        }
    }
 
    std::cout << "Najlepsza wartość: " << bestValue << "\nWybrane przedmioty: ";
    for (size_t i = 0; i < items.size(); i++) {
        if (bestMask & (1ULL << i)) std::cout << i << " ";
    }
    std::cout << std::endl;
    return 0;
}

OpenMP (kompilacja: g++ knapsack_openmp.cpp -o knapsack_openmp -fopenmp -O2)

  
#include <iostream>
#include <vector>
#include <cstdint>
#include <random>
#include <ctime>
#include <omp.h>
 
struct Item {
    int weight;
    int value;
    int priority;
};
 
std::vector<Item> generateItems(int numItems) {
    std::vector<Item> items;
    std::mt19937 rng(static_cast<unsigned>(std::time(nullptr)));
    std::uniform_int_distribution<int> wDist(1, 50);
    std::uniform_int_distribution<int> vDist(1, 100);
    std::uniform_int_distribution<int> pDist(1, 5);
 
    for (int i = 0; i < numItems; ++i) {
        items.push_back({wDist(rng), vDist(rng), pDist(rng)});
    }
    return items;
}
 
int evaluateSolution(const std::vector<Item>& items, uint64_t mask, int capacity, double priorityFactor, bool& valid) {
    int totalWeight = 0;
    int totalValue = 0;
    for (size_t i = 0; i < items.size(); i++) {
        if (mask & (1ULL << i)) {
            totalWeight += items[i].weight;
            totalValue  += items[i].value + static_cast<int>(items[i].priority * priorityFactor);
            if (totalWeight > capacity) {
                valid = false;
                return 0;
            }
        }
    }
    valid = true;
    return totalValue;
}
 
int main() {
    int numItems = 30;
    int capacity = 400;
    double priorityFactor = 0.5;
 
    std::vector<Item> items = generateItems(numItems);
    uint64_t totalSubsets = 1ULL << numItems;
 
    int bestValue = 0;
    uint64_t bestMask = 0;
 
    #pragma omp parallel
    {
        int localBestValue = 0;
        uint64_t localBestMask = 0;
 
        #pragma omp for schedule(dynamic)
        for (uint64_t mask = 0; mask < totalSubsets; ++mask) {
            bool valid = false;
            int value = evaluateSolution(items, mask, capacity, priorityFactor, valid);
            if (valid && value > localBestValue) {
                localBestValue = value;
                localBestMask = mask;
            }
        }
 
        #pragma omp critical
        {
            if (localBestValue > bestValue) {
                bestValue = localBestValue;
                bestMask = localBestMask;
            }
        }
    }
 
    std::cout << "Najlepsza wartość: " << bestValue << "\nWybrane przedmioty: ";
    for (size_t i = 0; i < items.size(); i++) {
        if (bestMask & (1ULL << i)) std::cout << i << " ";
    }
    std::cout << std::endl;
    return 0;
}

Implementacja w CUDA (kompilacja: nvcc knapsack_cuda.cu -o knapsack_cuda)

  
#include <iostream>
#include <vector>
#include <cstdint>
#include <random>
#include <ctime>
#include <cuda.h>
#include <cuda_runtime.h>
 
struct Item {
    int weight;
    int value;
    int priority;
};
 
std::vector<Item> generateItems(int numItems) {
    std::vector<Item> items;
    std::mt19937 rng(static_cast<unsigned>(std::time(nullptr)));
    std::uniform_int_distribution<int> wDist(1, 50);
    std::uniform_int_distribution<int> vDist(1, 100);
    std::uniform_int_distribution<int> pDist(1, 5);
 
    for (int i = 0; i < numItems; ++i) {
        items.push_back({wDist(rng), vDist(rng), pDist(rng)});
    }
    return items;
}
 
__global__ void evaluateKernel(const Item* items, int n, int capacity, double priorityFactor,
                               uint64_t totalSubsets, int* d_values) {
    uint64_t idx = blockIdx.x * blockDim.x + threadIdx.x;
    if (idx >= totalSubsets) return;
 
    int totalWeight = 0;
    int totalValue = 0;
 
    for (int i = 0; i < n; i++) {
        if (idx & (1ULL << i)) {
            totalWeight += items[i].weight;
            totalValue += items[i].value + static_cast<int>(items[i].priority * priorityFactor);
            if (totalWeight > capacity) {
                d_values[idx] = 0;
                return;
            }
        }
    }
    d_values[idx] = totalValue;
}
 
int main() {
    int numItems = 30;
    int capacity = 400;
    double priorityFactor = 0.5;
 
    std::vector<Item> h_items = generateItems(numItems);
    uint64_t totalSubsets = 1ULL << numItems;
 
    Item* d_items;
    cudaMalloc(&d_items, numItems * sizeof(Item));
    cudaMemcpy(d_items, h_items.data(), numItems * sizeof(Item), cudaMemcpyHostToDevice);
 
    int* d_values;
    cudaMalloc(&d_values, totalSubsets * sizeof(int));
 
    int blockSize = 1024;
    int gridSize = (totalSubsets + blockSize - 1) / blockSize;
 
    evaluateKernel<<<gridSize, blockSize>>>(d_items, numItems, capacity, priorityFactor, totalSubsets, d_values);
    cudaDeviceSynchronize();
 
    std::vector<int> h_values(totalSubsets);
    cudaMemcpy(h_values.data(), d_values, totalSubsets * sizeof(int), cudaMemcpyDeviceToHost);
 
    int bestValue = 0;
    uint64_t bestMask = 0;
    for (uint64_t i = 0; i < totalSubsets; ++i) {
        if (h_values[i] > bestValue) {
            bestValue = h_values[i];
            bestMask = i;
        }
    }
 
    std::cout << "Najlepsza wartość: " << bestValue << "\nWybrane przedmioty: ";
    for (int i = 0; i < numItems; i++) {
        if (bestMask & (1ULL << i)) std::cout << i << " ";
    }
    std::cout << std::endl;
 
    cudaFree(d_items);
    cudaFree(d_values);
    return 0;
}

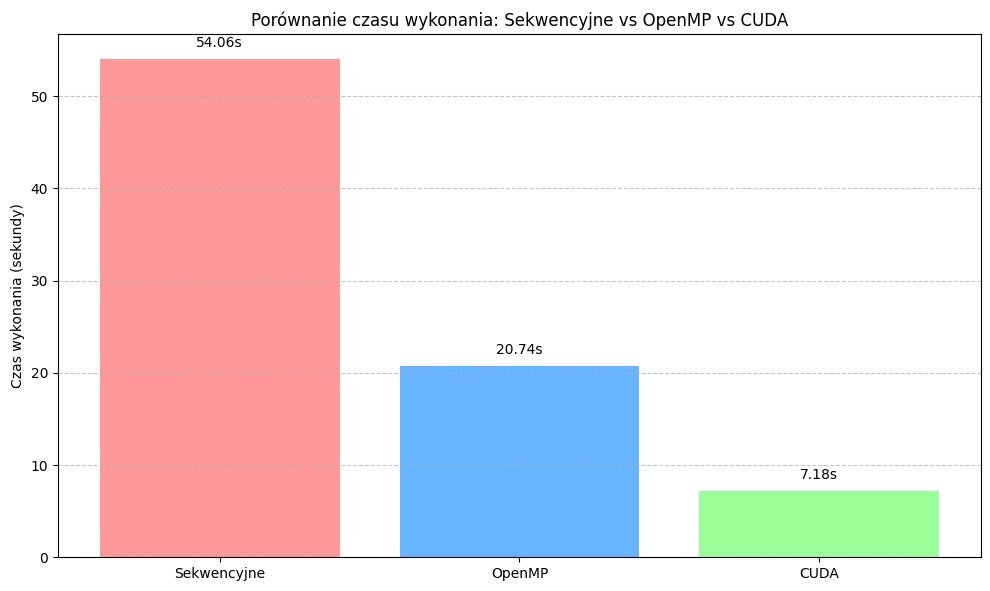
Porównanie czasu wykonania poszczególnych implementacji

Literatura

CUDA for Engineers: An Introduction to High-Performance Parallel Computing (Duane Storti)
Multicore and GPU Programming: An Integrated Approach (Gerassimos Barlas)
Programming in Parallel with CUDA: A Practical Guide (Richard Ansorge)

This post is licensed under CC BY 4.0 by the author.